
The half life period for a first order reaction is independent of initial concentration.
14C is radio active, its half life period is 5730 years. As long as the organism is living the ratio of 14C to 12C is the same as in the atmosphere. But when the organism dies, the intake of carbon stops and 14C starts disintegrating and then its amount starts decreasing according to its half life. In 5730 years the amount of 14C will become half its value when it was living. Thus if the amount of 14C can be analysed in the sample using the first order kinetics it is possible to calculate the age of the sample.
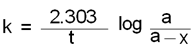
Where K = rate constant which is known
a = the initial concentration or the amount,
a-x = what is left in time t, and t1/2 = 0.693/k
Example:
When a piece of wood was analysed it was found to contain 25% of the 14C that should be normally present. The half life period of 14C is 5730 years. Find the age of the sample
Step 1: From t1/2 find k.
k =0 .693/5730 = 0.00012094Step 2: In the first equation a/a-x would be 100/25 = 4
Step3: In the first equation t is the only unknown factor simplify, the answer is: 11465 years .
Photosynthesis
Plants take in water and CO2 and with the help of solar radiation convert it to glucose( which will be generally stored in the form of starch). How do we know that CO2 is involved? Simple.
Grow a plant in a controlled atmosphere. Feed in CO2 containing an isotope of C. after several days analyse a leaf from the plant for the presence of the isotope of C. Its presence will be an indication of the fact that CO2 is involved in photosynthesis.
Source: Asimov on Chemistry